高等学校工業 機械設計/機械要素と装置/歯車

まず、平歯車から説明する。

平歯車の動き

平歯車とは、 歯が軸に対して、平行方向に歯が付く通常の歯車である。軸方向に対してねじれや傾斜などが無い歯車である。

• ピッチ円とは

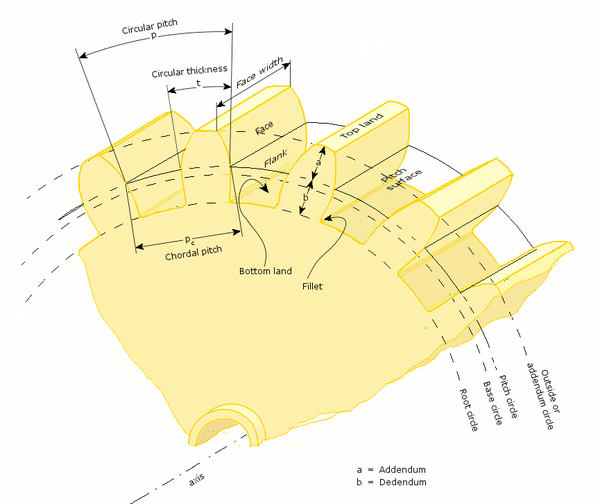
歯の接触してる接触点の軸からの距離は、回転中に変わるので、そのままでは計算が煩雑であり、不便である。なので、代表的な直径を選びたい。 歯車を、近似モデルで、摩擦車のような転がり摩擦をする円柱で近似すると、直径の計算が便利である。 このように歯車を転がり摩擦で伝動する円柱に近似したときの、その円柱の円周をピッチ円（pitch circle）といい、そのピッチ円の直径をピッチ円直径という。 ピッチ円のことを、基準円とも言う。

歯車用語の基礎

• ピッチ円直径（pitch diameter）

ピッチ円の直径のこと。dで現すことが多い。基準円直径ともいう。 名前が基礎円直径と似てるが、基準円と基礎円とは、別物なので注意。基礎円直径は、インボリュートを書くときの円柱の直径のこと。平歯車の場合は、歯底円の近くの直径になる。歯底円とインボリュートの基礎円とは異なるので混同しないように注意。

• モジュール （module）

メートル系の規格を採用してる国では、歯車の歯の大きさを表すのに、これから説明するモジュールという値を用いるのが一般である。定義は、歯数をzとして基礎円直径をd[mm]とした場合、モジュールは、

m=d/z

である。２つの歯車を噛み合わせる場合は、両歯車のモジュールを等しくさせる必要がある。 歯の大きさは、モジュールの値が大きいほど歯の大きさが大きくなる。

後述するが、歯車の歯先円直径は、インボリュート歯車の場合、

d_a ＝ d + 2m

と定められている。

歯形曲線

• 歯形曲線の種類

インボリュート歯車による力の伝達

歯形の曲線には、インボリュートという曲線が、一般に用いられることが多い。 インボリュートとは、円筒に糸を巻きつけて、ゆるみなく引きほどいていったときに、糸の先端が描く曲線。 この作図のときの巻きつけた円筒に相当する円を、基礎円（base circle）という。名前が基準円（ピッチ円）と似ているが別の円なので、間違えないように。

インボリュート歯形は、歯車の歯形では標準的に使われ、ほとんどの歯車の歯形はインボリュート歯形である。 歯形には、インボリュートの他にも、サイクロイド歯形、トロコイド歯形、円弧歯形などの歯形もあるが、特に断らない限り本書ではインボリュート歯形を例に説明する。

インボリュート曲線の幾何学

• 
  インボリュート曲線
• 
  糸を解く様子
• 
  基礎円の付近でのインボリュート拡大図

インボリュートの幾何学的な特徴として、インボリュート曲線と、その基礎円との接線とは、直角（=90°）で直交する、という性質が有る。なお後述するが、その結果、インボリュート歯車の作用線と歯形曲線とは、直交をする。

インボリュートの法線と基礎円の接線

証明は以下の通り。

• 定理

インボリュート曲線と、その基礎円との接線とは、直角（=90°）で直交する。

• 証明

そもそも円とは、正多角形の角数を無限に大きくしたものでもある。（小学校などで円の面積の公式を学んだ時の論法を思い出そう。） 証明の方針を述べると、まず、この正多角形に糸を巻きつけて、糸をゆるみなく引きほどいていったときに、糸の先端が描く曲線について、定理を証明すれば良い。 そのあとに、角数を無限大に増やせば、円の場合について証明ができる。

インボリュート曲線の、多角形化した場合のモデル。図は6角形に巻きつけた糸を解いていく場合。60度、ほどくごとに、半径が変わるが、たとえ半径が変わっても、接線と半径との直交関係は同じままである。

まず、正六角形に糸を巻きつけた場合で考えよう。糸をほどくと、60°ほどくたびに、半径が変わるが、それであっても、正六角形の各頂点を中心とした円弧の組み合わせで、ほどいた曲線を表現できる。そして、円弧の接線と、その接点を通る円弧の半径とは直交するという幾何の定理（いわゆる「接弦定理」の一例。）がある。

接弦定理とは、「円の接線とその接点を通る弦が作る角は、その角の中にある弧に対する円周角に等しい」という定理。弦が円の中心を通る場合の円周角は、円周角の定理より円周角が90°なので、接弦定理により、円周角と等しい「円の接線とその接点を通る弦が作る角」も90°になる。

したがって、接弦定理と円周角の定理により、正多角形に糸を巻きつけた場合の糸の軌跡は、円弧で表現できる糸の軌跡と、円弧の半径に相当する糸とは、直交をする。 正六角形の場合は糸を 60°ほどくたびに、円弧の中心位置と円弧の半径長さが変わるが、その場合でも、接線の方向は変わらないので、半径と接線とが直交するという関係も変わらない。

このほどいた時に半径長さが変わる現象は、インボリュート曲線では、ほどいた糸の長さが、ほどいた角度に応じて変わり続けることに相当する。だから、円に巻きつけた糸をほどいたインボリュート曲線でも、糸と軌跡との直交関係は変わらないということに対応する。

（※ 数学の「微分積分学」や「微分幾何学」などの数学教科書を読んでも、インボリュートの糸と軌跡の直交関係が証明されておらず、暗黙の前提として、直交関係を利用している。要するに、日本の数学者が、インボリュートの証明をきちんと理解していない。）

上述のようなインボリュートの多角形モデルのことを何と言うのかは、現時点（2021年）の編集では不明だが、サイクロイドを同じような考え方で正多角形で近似したものを「離散サイクロイド」と呼ぶ数学者もいる。この呼び方に習えば、上述のようなインボリュート曲線の多角形モデルのことは「離散インボリュート」という呼び方になるだろう。

以上は正六角形を例に説明したが、同様の証明が、正四角形でも正八角形でも、正多角形でも成り立つ。正多角形の角数を無限大にすれば、円になる。よって、インボリュート曲線の基礎円の接線とインボリュート曲線とは直角に直交する。（証明、おわり。）

• 余談

かさ歯車などの歯形に用いられるインボリュート等についても、同様の証明が、円と正多角形との場合だけでなく、円錐と角錐との場合も成り立つので、かさ歯車などについてインボリュートを拡張する場合は、以上の証明での「正多角形」を「正多角錐」に置き換えれば良い。

直交座標でのインボリュートの式の導出

もし、読者が高校三年レベルの微分積分とベクトルと三角関数との知識を知っていれば、座標幾何学的な計算を用いて、より詳細に、インボリュートと基礎円の接線との直交を証明できる。 もし読者がそれらをまだ知らなければ、この節は読み飛ばして頂きたい。

まず、直交座標上での式インボリュート曲線の式は、媒介変数表示を用いて以下の式である。次の式で、θは、基礎円上での、ほどかれた角度に相当し、θの単位はラジアン表示（弧度法）である。

${\begin{cases}x=a(\cos \theta +\theta \sin \theta ),\\y=a(\sin \theta -\theta \cos \theta )\end{cases}}$

これを導出しよう。

• 導出

まず、インボリュート曲線で、基礎円上で角度θだけ糸をほどいた場合の、基礎円上の糸の根本の位置ベクトルは、

$(x_{b},y_{b})=(a\cos \theta ,a\sin \theta )$

である。

ほどいた糸の長さはラジアン単位の定義よりa θであることが分かる。糸の方向については、さきほど初等幾何で証明したインボリュートの定理により、糸と基礎円の半径方向とは直交するので、つまり、方向ベクトルは、

$(x_{d},y_{d})=(\sin \theta ,-\cos \theta )$

である。ほどいた糸の長さはaθであったので、結局、ほどいた糸の、基礎円上の根本から糸の先端までのベクトルを(x_s,y_s)とすれば、

$(x_{s},y_{s})=a\theta (\sin \theta ,-\cos \theta )=(a\theta \sin \theta ,-a\theta \cos \theta )$

である。基礎円の根本の位置ベクトル(x_b,y_b)と、ほどいた糸のベクトル(x_s,y_s)とを組み合わせれば、インボリュートの直交座標上でのベクトル式(x,y)が導出される。

$(x,y)=(a\cos \theta ,a\sin \theta )+(a\theta \sin \theta ,-a\theta \cos \theta )=(a\cos \theta +a\theta \sin \theta ,a\sin \theta -a\theta \cos \theta )=a(\cos \theta +\theta \sin \theta ,\sin \theta -\theta \cos \theta )$

したがって、

$(x,y)=a(\cos \theta +\theta \sin \theta ,\sin \theta -\theta \cos \theta )$

以上で導出は、おわり。

直交座標でのインボリュートと基礎円接線との直交性の導出

インボリュートの接線ベクトルを求め、この説ベクトルと、糸の根本から先端までのベクトルとの直交性を調べるため、ベクトルの内積を計算すれば良い。 まず、軌跡の位置ベクトルは、

$(x,y)=a(\cos \theta +\theta \sin \theta ,\sin \theta -\theta \cos \theta )$

である。接線ベクトルを求めるため、軌跡の位置ベクトルをθで微分すれば、

$(x',y')=a(\theta \cos \theta ,\theta \sin \theta )$

基礎円上の根本から糸の先端までのベクトル(x_s,y_s)の式は、

$(x_{s},y_{s})=(a\theta \sin \theta ,-a\theta \cos \theta )$

でったので、直交性を調べるため、接線ベクトル(x',y') との内積を取れば計算すればいい。内積を計算すると、

$(x',y')\cdot (x_{s},y_{s})=a^{2}(\theta ^{2}\cos \theta \sin \theta -\theta ^{2}\sin \theta \cos \theta )=0$

となり、内積がゼロになるので、軌跡と基礎円の接線とが直交することが分かる。

※ 上述の考察から分かるように、歯車は一般的に、歯面どうしが滑りながら押し付けあっているので、潤滑が必要である。

作用線

インボリュート歯車では、噛み合う歯車の接触点の軌跡（この軌跡を作用線という）が、円のインボリュートの幾何学的な性質により、両歯車の基礎円の共通接線になる。 なので、その結果として、もし取り付けの際に両歯車の軸中心間の距離が少しずれても、インボリュート歯車どうしなら、一定の回転速度でかみ合うので、便利である。

• 
  作用線（Line of action）
• 
  接触点と作用線と歯形曲線の関係

なぜ、軸中心が少しずれても、一定の回転速度でかみ合うかというと、もし軸中心の距離が少しずれても軌跡としている共通接線が少し変わるだけで、共通接線を軌跡とするという性質が変わらないからである。

また、以上の結果から、インボリュート歯車では、歯車の回転速度が一定になる。

• 圧力角

圧力角

基準円の共通接線と作用線のなく角を圧力角（pressure angle）という。 一方、歯面の法線と半径方向（基準円の法線）とのなす角を英語圏では"profile angle"とよび区別することがある。インボリュート歯車の場合、この圧力角と"profile angle"は等しくなる。 ただし、日本産業規格のJIS B 0102-1:2013「歯車用語－第1部：幾何形状に関する定義」（4.1.5.2）では、圧力角の定義が異なり、英語圏での"profile angle"に相当する、歯面の法線方向と半径方向の角度の定義を持って、「圧力角」の定義としているので、注意。

「en:w:Pressure angle」および「en:w:Profile angle」も参照

バックラッシ

バックラッシュ

歯車の、かみ合ってる歯の後方にできる隙間のことをバックラッシ（Backlash, バックラッシュとも呼ぶ）という。この隙間は必要であり、バックラッシによって歯車は滑らかに動くことができ、また潤滑や誤差の吸収や熱膨張の吸収にも必要である。しかし、ある方向に回転していた歯車を逆方向に回転させたときに、バックラッシの長さの分だけ、かみ合わない状態が生じ、その結果として衝撃が生じることがある。 歯車へのバックラッシの設け方は、二つの方法があり、取り付け時に歯車の中心間距離を少しだけ広げる方法と、歯車製作時に歯を少しだけ細く作る方法とがある。

歯を細く作りバックラッシを設ける方法では、製作時の工具による歯切りのときに、切込み深さを標準の切込み深さよりも少し深くして切り込むことで、歯車を少しだけ細くしてバックラッシを設ける。

遊星歯車機構

遊星歯車機構

遊星歯車機構（ゆうせいはぐるまきこう、英語：planetary gear mechanism）とは太陽歯車（sun gear）を中心として、遊星歯車（planetary gear）が、かみ合いながら自転しつつ公転する構造を持った機構である。 これら太陽歯車と遊星歯車に、さらに内歯車を付け加えた機構を含めて、遊星歯車機構と呼ぶ場合もある。

回転比の式の導出

転がっている剛体は、地面との接触点を中心にして、自転をしている。

公転と自転と回転数の関係式を計算する際、太陽歯車と遊星歯車からなる遊星歯車機構のモデルは、角柱の周りを別の角柱（ただし、両柱の一辺の長さは同じとする。）が滑りなく公転するモデルで、初等幾何的に計算できる。 このとき、角柱の辺の数は、各歯車の歯数と同じにすれば良い。ところで、回転している剛体の回転の中心点を、自転や公転は特に区別せず、幾何学の用語で回転中心（rotation center）という。この角柱モデルでの説明では、自転と公転を区別することにする。遊星側の角柱の自転の中心は、転がっている遊星側の角柱と太陽側の角柱との接触点になっている頂点の位置になる。（一時的に点接触ではなく、線接触になる瞬間があるが、虫をする。）なお、今回のモデルにかぎらず、一般に、平面の転がっている剛体の回転中心は、剛体と平面との接触点になる。証明を知りたければ、多角形を転がした場合を考えれば良い。 説明の都合のため、角柱は、遊星側・太陽側の両方とも正多角柱とする。ふたつの角柱は、辺の数は、違っていても構わないが、一辺の辺の長さは同じとする。

自転の定義と公転の定義

なお、今までの説明で特に断らなかったが、このモデルでの剛体における自転の定義は、運動をした剛体上のある1個の線分が、座標系のx軸などの基準線（これは運動によらず固定とする。）となす角度が、運動の前後で、どのくらいの変化量をしたかで定義する。この角度は、剛体上のどの線を選んでも変わらない。もし剛体上で選んだ線分の種類によって、運動後の基準線との角度変化量が異なったとすると、回転演算を逆算すると剛体の各質点の間隔が変わったことになり、剛体が変形したことになるので、もはや剛体の定義と矛盾する。剛体の定義は、質点の集まりとしての物体のうちで、質点相互の間隔が変わらないもののことを言う。 また、このモデルでの剛体の公転の定義は、剛体上の一点と基準点（これは運動によらず固定とする。）とのなす角度が、運動の前後で、どのくらい変化をしたかで定義をする。剛体上の、どの点を選んでも、自転の場合と同様に、公転の結果は変わらない。もし点の種類によって公転の角度変化量が変わったとすると、自転の定義の場合と同様に、回転演算を逆算すると物体が変形したことになり、やはり剛体の定義と矛盾する。

瞬間中心

なお、回転中心と似たような概念で、機械工学には瞬間中心（instant center）という概念があるが、これは剛体の速度分布から求めた中心点である。必ずしも自転の中心と一致するとは限らないので、読者は混同しないように気をつけるべきである。他にも混同しやすい例として、縮閉線（インボリュート展開の逆操作によってもとめた点の軌跡のこと）の中心や、曲率中心（軌跡を静止した円で近似した場合の、その円の中心点）と間違えやすいが、これらとも瞬間中心は異なる概念である。 平面の上を円盤や円柱が転がるときは、平面と円との接触点を瞬間中心と見なせる。この場合は、自転の中心と瞬間中心がおなじになる。

• 
  瞬間中心の図1
  点A₁,B₁が移動して点A₂,B₂へ移った場合、図中の点Pが瞬間中心である。
  遊星歯車の頭文字"p"とは無関係なので混同しないように。（偶然の一致）
• 
  瞬間中心の図2
  図中の矢印は速度方向を表している。速度の垂直線の交点である点I が瞬間中心である。

角柱モデルでの遊星機構の説明

遊星歯車機構の惑星歯車の自転と太陽歯車の公転の回転比についての、多角形モデルの外角で表した場合の原理図。

まず、太陽側の角柱を静止させて、固定させたモデルで検討をする。説明の簡単化のため、内歯車をもつ場合の機構は、別途、後述する。 さて、太陽側の歯数をZ_sとしよう。これをモデル化した角柱は、正S角柱だとする。遊星側の歯数はZ_pとしよう。これをモデル化した角柱は、正P角柱だとする。 遊星側の角柱が、太陽側の角柱を接触しながら転がって、ある一辺から隣の辺に移る際の遊星側の角柱の自転角度は、幾何学的に考えれば、遊星側の角柱の外角E_pに太陽側の角柱の外角E_sを足した角度E_p+E_sと同じである。公転が時計回りなら自転も時計回りなので、公転の向きと自転の向きは同じ向きであるので、計算では足しあわせて良い。 そして、太陽側の正多角形の各辺の外角は

(${\frac {360}{S}}$)°

である。つまり、

$E_{s}={\frac {360}{S}}$

同様に、遊星側の各辺の外角も、

$E_{p}={\frac {360}{p}}$

である。これを足しあわせた角度、E_p+E_sが、一辺を転がった時の自転の量だから、この量は、

$E_{p}+E_{s}={\frac {360}{S}}+{\frac {360}{P}}$

で表される。 公転の角度については、遊星側が太陽側の一辺を転がって隣の辺に移るたびに、太陽側の角柱の外角と同じだけ公転する。つまり、遊星側が一辺を移るたびに、遊星側の角柱の公転量は、${\frac {360}{S}}$ °だけ公転をする。

自転と公転の比例係数を取れば、結局、遊星側の角柱の自転（rotation）と公転(revolution)の比は

${\frac {rotation}{revolution}}={\frac {P+S}{P}}=1+{\frac {S}{P}}$

になる。

余談だが、摩擦車などの周りを滑りなく転がす場合も同様の手法で自転と公転の比を、幾何学的に証明できる。この場合は、摩擦車の円周長さを、角柱の角数に置き換えて、同様に証明すれば良い。

次に、円形の枠の内側に歯がついた内歯車の場合のモデルを説明する。この場合は、内歯車のモデルは、穴が空いた型枠のモデルで考えれば良い。正多角形の穴が空いた型枠を、内歯車のモデルにする。

多角形の型枠の中を、別の多角形が転がる問題を考えよう。説明の便宜上、型枠の角数もS角形としよう。（太陽sunの頭文字を用いるのは不合理だが、太陽歯車の公式と内歯車の公式の2つの公式を対照的に比較できるので、この説明では型枠を正S角形とする。） まず、外側の型枠の正多角形Sは固定されて、内側の正P角形が転がる場合を考えるとする。 遊星歯車の公転と自転の方向は、内歯車のモデルの場合では、逆向きになる。 したがって、遊星側の角柱の公転と自転の比は、

${\frac {rotation}{revolution}}={\frac {P-S}{P}}=1-{\frac {S}{P}}$

になる。

（※ 一般的な大学レベルの機械工学の教科書では、この歯車のまわりを公転する歯車の図形問題で、外角のモデルを採用しておらず、公式丸暗記である。また、数学書や数学啓蒙書などでも、外角モデルを採用しておらず、円のユークリッド幾何学などから「証明」している。数学の啓蒙書に、ときどき「十円玉の円周に、別の十円玉を接触させて、すべらずに十円玉を1回公転させたら、十円玉が公転を何回するだろうか？」という問題が書いてあって、その証明で、円のユークリッド幾何学などから「証明」している。（「証明」だと、その数学書は主張している。もちろん、円のモデルでは、楕円のまわりで楕円を転がす場合に拡張されると、円のユークリッド幾何学では手におえず、もはや理解不可能になる。また、円錐に接触させた別の円錐を転がす問題でも、手に負えなくなる。要するに、日本の数学者が、円的な図形の周りを公転する図形の問題についての、外角モデルの証明を知らない。要するに、日本数学界が、何も知らない。）

遊星機構における自転と公転の回転比の公式

最終的に機械技術者が知りたいのは、幾何学の角柱の性質ではなく、機械工場での実務の歯車計算である。だから、上記の式を歯数Z_sおよびZ_pを用いた表現に直そう。 すると、静止した外歯車の周上を遊星歯車が転がる場合の自転（rotation）と公転（revolution）の比は、

${\frac {rotation}{revolution}}={\frac {Z_{p}+Z_{s}}{Z_{p}}}=1+{\frac {Z_{s}}{Z_{p}}}$

となる。 静止した内歯車の枠内を遊星歯車が転がる場合の自転と公転の比は、

${\frac {rotation}{revolution}}={\frac {Z_{p}-Z_{s}}{Z_{p}}}=1-{\frac {Z_{s}}{Z_{p}}}$

になる。

太陽歯車を回転させた場合

二つの外歯車について、太陽側を回転させて、遊星側を固定した場合は、ただの平歯車同士の回転である。とくに目新しい説明事項はないので、これについては説明を終える。

太陽歯車と遊星歯車と内歯車を、公転を止めて自転させた場合

かさ歯車の場合

かさ歯車の使用例
（画像では、2個のかさ歯車が噛み合っている。）

かさ歯車の場合で、自転と公転の比を求めたい場合は、角柱における外角の代わりに、円錐のとなりあう2個の斜面の法線（垂直線）の変化量を、外角の代わりとして用いて同様に計算すればよい。あるいは、便宜上だが、角錐や円錐のような立体図形でも、外角の定義を法線の概念によって、拡張できると見なすこともできる。ただし、図形が可展面（「かてんめん」。その図形を紙で作った場合に、切れ目を入れれば、平らな平面にできる図形のこと）である必要がある。

歯の強さ

曲げ強さ

sが危険断面。tが円ピッチ。

まず、歯が太いほうが、直感的に言って、曲げに強いだろう。 太さとは単純に考えれば、歯車の幅をbとし、円周方向の長さに相当する円ピッチをt とすれば、単純計算で歯の太さはbt であろう。詳しくは、あとで計算する。

また、歯車の最も弱い部分は、根本のくびれてる部分だから、この断面を定義し（危険断面と言う。右図ではsと表されてる。）その断面での、せん断応力を考えればいい。 なお、危険断面の位置と、円ピッチの位置とは異なるが、単純計算なので、歯の太さについては、とりあえずはbtで近似できると考えることにする。さて、せん断応力の算出には、歯を片持はりと見なして計算すれば良いだけである。

かみあい率については、計算の単純化のため、考えない。曲げ強さの計算では、１枚の歯に力がかかるとする。それに強さを計算するのならば、最悪の場合である１枚の歯にのみ力がかかる場合を計算するのが合理である。一般に，ピッチ円の接線方向の力が1枚の歯先に作用するものと考える。

とすると、直感的には、歯の強さの式は、次のような形の式になるだろう。

$F=\sigma bty$

これをルイスの式という。ただし、y は歯形係数といい、圧力角などの形状などに依存する係数である。詳しくは後述する。

あるいは、円ピッチt の代わりにモジュールm で、ルイスの式を定義することもある。こちらの定義の場合のほうが多い。つまり、

$F=\sigma bmy$

である。

Hoferの危険断面

歯の曲げ強さ

歯でもっとも破壊しやすい場所の曲げ強さを考えれば、じゅうぶんである。そのような、もっとも弱い場所は、歯の根元付近にある。この面を定義するため、歯形中心線（歯先の中央点から、半径方向に歯車中心点へと下ろした線。）と角30°をなして歯元に下ろした直線が、歯元の歯形曲線と内接する2点を点B，点Cとする。この線BCからなる断面を、歯の危険断面という。危険断面とは、強さの解析などの際、もっとも破壊しやすいと予測される場所のことである。歯車の強さの計算で、この場所が最も弱いと考える方法を、Hofer （ホーファー）の30°接線法という。

歯に働く力

では、解析を進める。

この危険断面上の円周接線方向の歯厚を s とする。 歯の円周方向の力がF[N]だとしよう。これは伝達動力P [W]から周速度v [m/s]を割れば求められる。 つまり、まずPやvの実験値から、

F=p/v

が求まる。

これは、歯面で歯が受けた力（F_nとする）のうち、まず、歯を曲げようとする力はcosβ方向のぶんのみである。sinβ方向は、歯を中心軸へ向けて圧縮しようとする方向であり、曲げ方向ではない。

よって、

歯を曲げようとする力F₁ は、

F₁ ＝ F_n cosβ

である。

あとは、歯面で歯が受けた力 F_n さえ、求めればよい。さきに結論を言うと、

F ＝ F_n cosα

である。なぜなら歯が受けた力F_n のうち、歯車の回転に寄与するのは圧力角a [rad]の余弦cos α の分だけだからである。

さて、われわれが最終的に求めたいのは、歯の曲げ強さであり、そのため歯車に関する力で最終的に求めたいのは、曲げ方向の力 F₁ である。

わざわざFnやFを求めるのは、たんに直接はF1を測定できないので、しかたなく実験値から導出できるFとの関係式を求めたわけである。

つまり、実験から導出したFをもとに、最終的にF1を求めればよい。では、その計算作業をしよう。

${\begin{cases}\\\\\end{cases}}$

F1 ＝ Fn cosβ F ＝ Fn cosα

この連立方程式を解けばよく、Fをもとに、最終的にF1を求めればよい。

1段目の式を、2段目の式で割れば、

${\begin{cases}\\\\\end{cases}}$

${\frac {F_{1}}{F}}={\frac {\cos \beta }{\cos \alpha }}$

移項して、

$F_{1}=F{\frac {\cos \beta }{\cos \alpha }}$

である。

歯の曲げ強さ

次に、曲げモーメントM の大きさを考える。ここで、「モーメント＝力*距離」の距離を考えるため

L ：力の作用線と歯形中心線との交点から危険断面までの距離

とLを設定すれば、曲げモーメントM は、

$M=F_{1}L$

である。

いっぽう、せん断力によって生じる曲げ応力σ と曲げモーメントMの関係式は、断面係数Z を用いて、

$M=\sigma Z$

であった。 危険断面は、長方形断面と見なしてよく、長方形断面の断面係数の公式はZ=(1/6)bh^2 である。今回の歯車の場合では、危険断面の厚さをsとしたので、断面係数は$Z=(1/6)bs^{2}$ である。これを曲げモーメントと断面係数の式に代入し、

$\sigma ={\frac {M}{Z}}={\frac {F_{1}L}{Z}}=({\frac {F_{n}L}{Z}}){\frac {\cos \beta }{\cos \alpha }}=({\frac {F_{n}6L}{bs^{2}}}){\frac {\cos \beta }{\cos \alpha }}$

さて、分母にb が出てるが、冒頭の歯の太さの単純計算では、歯の太さをモジュールm を用いてbm で近似したのであった。だから、分子と分母の両辺にモジュールm を導入して、歯の太さの項bm を分母に用いた式に変形しよう。すると、やや後知恵な変形だが、次のように変形できる。

$\sigma ={\frac {F_{n}6L}{bs^{2}}}{\frac {\cos \beta }{\cos \alpha }}={\frac {F_{n}6(L/m)}{bm(s/m)^{2}}}{\frac {\cos \beta }{\cos \alpha }}$

$={\frac {F_{n}}{bm}}{\frac {6(L/m)}{(s/m)^{2}}}{\frac {\cos \beta }{\cos \alpha }}$

ここで、

$Y={\frac {6(L/m)}{(s/m)^{2}}}{\frac {\cos \beta }{\cos \alpha }}$

を歯形係数として定義する。導出のモジュールで分子と分母を導入する式変形が後知恵的だったが、歯形係数の次元を見ると、無次元量になってるので次元がある場合より一般的であり、導出の式変形には納得をして貰いたい。

文献によっては、上記の式の逆数に近い式によって与えられる場合もあるので、注意が必要である。また、圧力角を歯形係数の代わりに用いる場合もある。 もし、数表などから歯形係数の数値を引用する際に、誤って別の定義の歯形係数を用いてしまうと、計算結果が間違ってしまう。なので、数表で計算する場合は、歯形係数の定義にどの定義を用いているかを確認の上で用いること。

参考文献

1. 日本機械学会、『機械実用便覧』改訂第6版、丸善株式会社、2006年。
2. 林洋次ほか12名、『機械設計2』、実教出版、平成25年（西暦2013年）。（文部科学省検定済教科書）
3. 青山秀樹・中島尚正ほか5名、『機械設計学』初版、朝倉書店、1998年10月。
4. ウィキペディア記事『歯車』、参考時の記事のリビジョンは2013年8月7日 (水) 11:08の版‎。

1. 『機械実用便覧』は用語の確認などに使用。
2. 『機械設計2』は高校での教育範囲の確認および、最新の規格の確認に使用した。